ニューラルネットワークで重要な活性化関数の1つである「シグモイド関数」を紹介しています。理解のしやすいシグモイド関数をPythonで実装も行いながら紹介します。
シグモイド関数とは?
シグモイド関数のグラフ
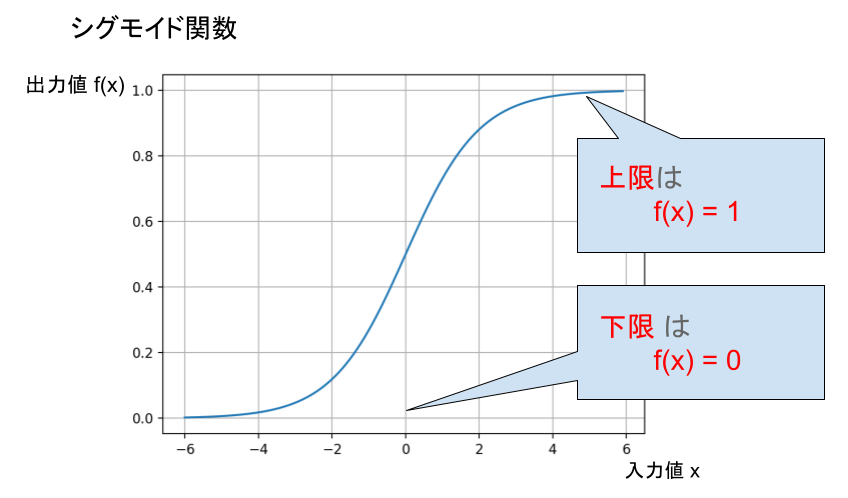
具体的には、
「x」が「0」のときは出力値「0.5」をとり、
その点から離れるにつれて「+1」か「-1」へ近づきます。
シグモイド関数は「x = 0」を中心としたなめらかで美しい曲線を描きます。
左右が点対称という観点からも、非常に利用しやすい活性化関数と考えられています。
活性化関数では、
今回の「シグモイド関数」や「ReLU関数」、最近登場した「Mish関数」などがよく用いられています。
その上で、「シグモイド関数」はニューラルネットワークを学ぶ上で非常に重要と言えます。
シグモイド関数はニューラルネットワークの活性化関数を理解する上で非常に重要なことから、
DeepLearningの入門書では、最初に取り上げられることが多いです。
シグモイド関数とステップ関数との違い
パーセプトロンが利用されていた頃までは、ステップ関数が一般的でした。
それ以降、活性化関数の発展につれて、
簡単に非線形的に処理できることから、シグモイド関数が一般的になりました。
シグモイド関数がステップ関数より優れているところは、微分できることにあります。
この微分できるといシグモイド関数の特性から、ニューラルネットワークの発展に繋がったわけですが、
微分の利用については、別の記事でまとめます。
シグモイド関数の数式
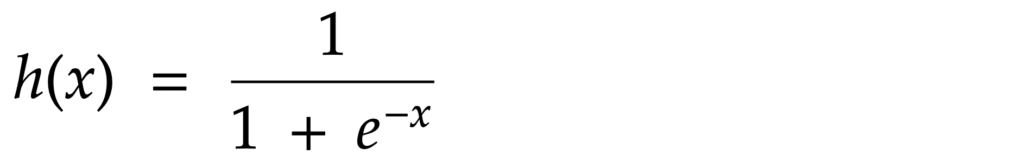
少し複雑ですが、
この数式であの美しい滑らかな曲線を描けることが、感動します。
Pythonで実装
実装
#sigmoid関数
import numpy as np
def sigmoid(x):
return 1./(1. + np.exp(-x))
if __name__ == '__main__':
print(sigmoid(0)) # 任意の数字を入力【実行結果】
0.55行目の「np.exp(-x)」で「e の -x乗」を表現しています。
コードは非常にシンプルですね。
【参考】ステップ関数をプロットするコード
下記は、matplotlibを使ってシグモイド関数を描画するコードです。
#シグモイド関数
import matplotlib.pyplot as plt
import numpy as np
import math
e = math.e
x = np.arange(-6, 6, 0.1)
y = 1./(1. + np.exp(-x))
plt.grid()
plt.plot(x, y)
plt.show()このコードを実行すると、下のグラフが生成されます。
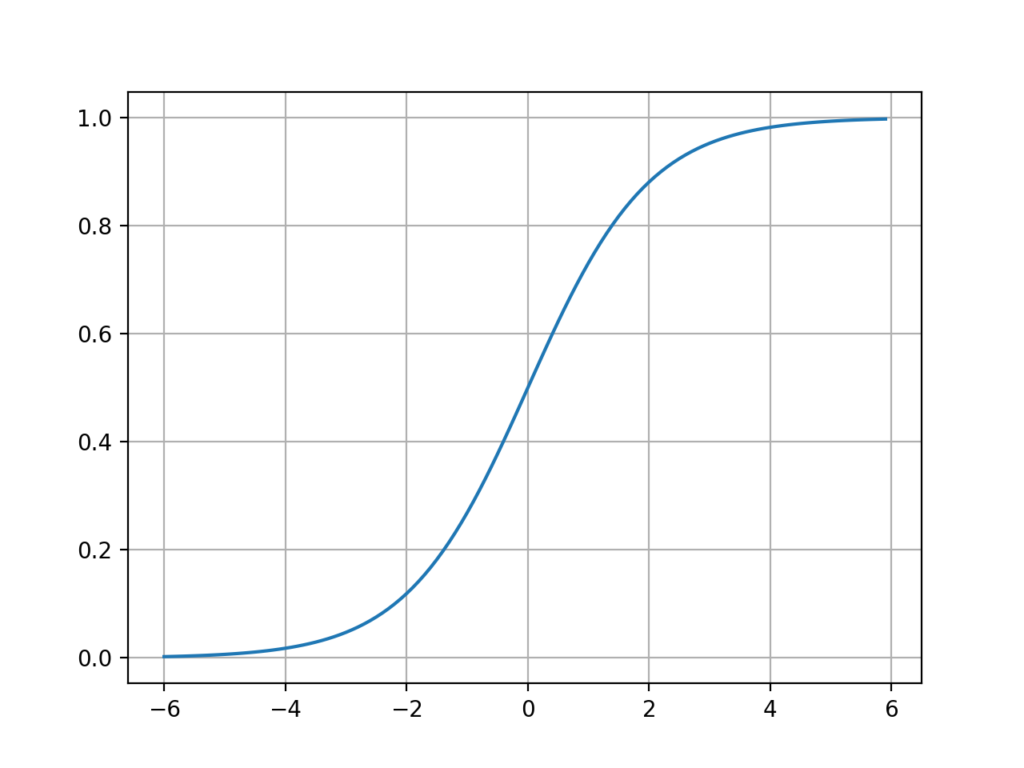
ということで本記事は、
ニューラルネットワークで非常に重要な、活性化関数の1つであるシグモイド関数を紹介しました。
最後まで読んでいただき、ありがとうございました!
ディープラーニングのおすすめ書籍
専門書としては異例の発行部数を誇る、素晴らしい書籍です(^^)
初心者の方から知識のある方まで、幅広い方に向けて書かれていますよ!\(^o^)/
超オススメのPC用品
PCを操作する上で、トラックボールマウスが非常におすすめです!
僕も感動したこのマウスを、騙されたと思って使ってみてください!(^^)
外部モニターで2倍以上の効率化が見込めます!
安いものだと、たったの1万円前後なのでおすすめですよー!\(^o^)/
 tetoblog
tetoblog 

